ACCELERATING EDUCATION: FEYNMAN

ACCELERATING EDUCATION: FEYNMAN: Πράγματι, όπως εκτίμησε και ίδιος ο Feynman στον πρόλογο του από τις διαλέξεις φυσικής, όταν διαπίστωσε ότι ο αριθμός των φοιτητών του ...

GEOLOGICAL TIME

GEOLOGICAL TIME

Dinosaurs did not find in Greece because the hole area was under the sea, during the Cretaceous period.

The Earth in My Pocket: an Introduction to Geology

How old is the earth?

Huge number, if we thouhgt that the earth was  existing for  24 hours, the human civilization  was created the last three seconds.

ACCELERATING EDUCATION: The ice cube in the right cup will sink !!!

ACCELERATING EDUCATION:
The ice cube in the right cup will sink !!!: The ice cube in the right cup will sink !!!

ACCELERATING EDUCATION: Motion and Force

ACCELERATING EDUCATION: Motion and Force: Calculate the forces and design the graph x-t!!!

Postulates of the Special Theory of Relativity

The problems that existed at the start of the twentieth century with regard to electromagnetic theory and Newtonian mechanics were beautifully resolved by Einstein’s introduction of the special theory of relativity in 1905. Unaware of the Michelson–Morley null result, Einstein was motivated by certain questions regarding electromagnetic theory and light waves. For example, he asked himself: “What would I see if I rode a light beam?” The answer was that instead of a traveling electromagnetic wave, he would see alternating electric and magnetic fields at rest whose magnitude changed in space, but did not change in time. Such fields, he realized, had never been detected and indeed were not consistent with Maxwell’s electromagnetic theory. He argued, therefore, that it was unreasonable to think that the speed of light relative to any observer could be reduced to zero, or in fact reduced at all. This idea became the second postulate of his theory of relativity. In his famous 1905 paper, Einstein proposed doing away with the idea of the ether and the accompanying assumption of a preferred or absolute reference frame at rest. This proposal was embodied in two postulates. The first was an extension of the Galilean–Newtonian relativity principle to include not only the laws of mechanics but also those of the rest of physics, including electricity and magnetism:

First postulate (the relati£ity principle): The laws of physics have the same form in all inertial reference frames. The first postulate can also be stated as: there is no experiment you can do in an inertial reference frame to determine if you are at rest or moving uniformly at constant velocity. 

The second postulate is consistent with the first: Second postulate (constancy of the speed of light): Light propagates through empty space with a definite speed c (3.00Χ10^8 m/s) independent of the speed of the source or observer. 

These two postulates form the foundation of Einstein’s special theory of relativity. It is called “special” to distinguish it from his later “general theory of relativity,” which deals with noninertial (accelerating) reference frames. The special theory, which is what we discuss here, deals only with inertial frames. The second postulate may seem hard to accept, for it seems to violate common sense. First of all, we have to think of light traveling through empty space. Giving up the ether is not too hard, however, since it had never been detected. But the second postulate also tells us that the speed of light in vacuum is always the same, no matter what the speed of the observer or the source. Thus, a person traveling toward or away from a source of light will measure the same speed for that light as someone at rest with respect to the source. This conflicts with our everyday experience: we would expect to have to add in the velocity of the observer. On the other hand, perhaps we can’t expect our everyday experience to be helpful when dealing with the high velocity of light. Furthermore, the null result of the Michelson–Morley experiment is fully consistent with the second postulate.

Einstein’s proposal has a certain beauty. By doing away with the idea of an absolute reference frame, it was possible to reconcile classical mechanics with Maxwell’s electromagnetic theory. The speed of light predicted by Maxwell’s equations is the speed of light in vacuum in any reference frame. Einstein’s theory required us to give up common sense notions of space and time, and in the following Sections we will examine some strange but interesting consequences of special relativity. Our arguments for the most part will be simple ones. 

Simultaneity

An important consequence of the theory of relativity is that we can no longer regard time as an absolute quantity. No one doubts that time flows onward and never turns back. But according to relativity, the time interval between two events, and even whether or not two events are simultaneous, depends on the observer’s reference frame. By an event, which we use a lot here, we mean something that happens at a particular place and at a particular time. Two events are said to occur simultaneously if they occur at exactly the same time. But how do we know if two events occur precisely at the same time? If they occur at the same point in space—such as two apples falling on your head at the same time—it is easy. But if the two events occur at widely separated places, it is more difficult to know whether the events are simultaneous since we have to take into account the time it takes for the light from them to reach us. Because light travels at finite speed, a person who sees two events must calculate back to find out when they actually occurred. For example, if two events are observed to occur at the same time, but one actually took place farther from the observer than the other, then the more distant one must have occurred earlier, and the two events were not simultaneous.

We now imagine a simple thought experiment. Assume an observer, called O, is located exactly halfway between points A and B where two events occur, Fig. 26–3. Suppose the two events are lightning that strikes the points A and B, as shown. For brief events like lightning, only short pulses of light (blue in Fig. 26–3) will travel outward from A and B and reach O. Observer O “sees” the events when the pulses of light reach point O. If the two pulses reach O at the same time, then the two events had to be simultaneous. This is because (i) the two light pulses travel at the same speed (postulate 2), and (ii) the distance OA equals OB, so the time for the light to travel from A to O and from B to O must be the same. Observer O can then definitely state that the two events occurred simultaneously. On the other hand, if O sees the light from one event before that from the other, then the former event occurred first. The question we really want to examine is this: if two events are simultaneous to an observer in one reference frame, are they also simultaneous to another observer moving with respect to the first? Let us call the observers O1 and O2 and assume they are fixed in reference frames 1 and 2 that move with speed v relative to one another. These two reference frames can be thought of as two rockets or two trains (Fig. 26–4). O2says that O1 is moving to the right with speed v, as in Fig. 26–4a; and O1 saysO2 is moving to the left with speed v, as in Fig. 26–4b. Both viewpoints are legitimate according to the relativity principle. [There is no third point of view that will tell us which one is “really” moving.]

Now suppose that observers O1 and O2 observe and measure two lightning strikes. The lightning bolts mark both trains where they strike: at A1 and B1 on O1's train, and at A2 and B2 on O2's train, Fig. 26–5a. For simplicity, we assume that O1 is exactly halfway between A1 and B1 and O2 is halfway between A2 and B2. Let us first put ourselves in O2's reference frame, so we observe O1 moving to the right with speed v. Let us also assume that the two events occur simultaneously in O2's frame, and just at the instant when O1 and O2 are opposite each other, Fig. 26–5a. A short time later, Fig. 26–5b, light from A2 and from B2 reach O2 at the same time (we assumed this). Since O2 knows (or measures) the distances) O2A2 and O2B2 as equal, knows the two events are simultaneous in the reference frame.

But what does O1 observer observe and measure? From our (O2) reference frame, we can predict what O1 will observe. We see that  O1 moves to the right during the time the light is traveling to O1 from A1 and B1. As shown in Fig. 26–5b, we can see from O2 our reference frame that the light from B1 has already passed O1 whereas the light from A1 has not yet reached O1. That is, O1 observes the light coming from B1 before observing the light coming from A1. Given (i) that light travels at the same speed c in any direction and in any reference frame, and (ii) that the distance O1A1 equals O1B1 then observer  O1 can only conclude that the event  at B1 occurred before the event at A1 The two events are not simultaneous for O1 even though they are for O2. We thus find that two events which take place at different locations and are simultaneous to one observer, are actually not  simultaneous to a second observer who moves relative to the first. It may be tempting to ask: “Which observer is O1 right, or O2 ” The answer, according to relativity, is that they are both right. There is no “best” reference frame we can choose to determine which observer is right. Both frames are equally good. We can only conclude that simultaneity is not an absolute concept, but is relative. We are not aware of this lack of agreement on simultaneity in everyday life because the effect is noticeable only when the relative speed of the two reference frames is very large (near c), or the distances involved are very large.

from: Giancoli 7th ed Physics Chapters, Ch 26 The special theory of relativity

Giannis Simantirakis Reczko

A PASSION FOR SYMMETRY: Special Theory of Relativity (from Giancoli's Phys...

A PASSION FOR SYMMETRY: Special Theory of Relativity (from Giancoli's Phys...: Postulates of the Special Theory of Relativity The problems that existed at the start of the twentieth century with regard to electr...

LIVE EXPERIMENTS SNAPCHAT : ACCELERATINGEDU

ACCELERATING EDUCATION: How do we correlate the Milankovitch orbital cycle...

ACCELERATING EDUCATION: How do we correlate the Milankovitch orbital cycle...:   Conceptual stratigraphic model  Combined with the movement of perihelion (the time at which the Sun is closest to Earth), it...

ACCELERATING EDUCATION: The Hopewell Rocks - OFFICIAL Time Lapse video of ...

ACCELERATING EDUCATION: The Hopewell Rocks - OFFICIAL Time Lapse video of ...

Subramanyan Chandrasekhar - Facts

Born: 19 October 1910, Lahore, India (now Pakistan)

Died: 21 August 1995, Chicago, IL, USA

Affiliation at the time of the award: University of Chicago, Chicago, IL, USA

Prize motivation: "for his theoretical studies of the physical processes of importance to the structure and evolution of the stars"

Field: astrophysics

Prize share: 1/2

Beauty and the Quest for Beauty in Science

All of us are sensitive to Nature's beauty. It is not unreasonable that some aspects of this beauty are shared by the natural sciences. But one may ask the question as to the extent to which the quest for beauty is an aim in the pursuit of science. On this question, Poincare is unequivocal. In one of his essays he has written:

The Scientist does not study nature because it is useful to do so. He studies it because he takes pleasure in it; and he takes pleasure in it because it is beautiful. If nature were not beautiful, it would not be worth knowing and life would not be worth living. . . . I mean the intimate beauty which comes from the harmonious order of its parts and which a pure intelligence can grasp.

And Poincaré goes on to say:

It is because simplicity and vastness are both beautiful that we seek by preference simple facts and vast facts; that we take delight, now in following the giant courses of the stars, now, in scrutinizing with a microscope that prodigious smallness which is also a vastness, and, now, in seeking in geological ages the traces of the past that attracts us because of its remoteness.

Commenting on these observations of Poincare, J.W.N. Sullivan, the author of perceptive biographies of both Newton and Beethoven, wrote (in the Athenium for May 1919):

Since the primary object of the scientific theory is to express the harmonies which are found to exist in nature, we see at once that these theories must have aesthetic value. The measure of the success of a scientific theory is, in fact, a measure of its aesthetic value, since it is a measure of the extent to which it has introduced harmony in what was before chaos.

It is in its aesthetic value that the justification of the scientific theory is to be found, and with it the justification of the scientific method. Since facts without laws would be of no interest, and laws without theories would have, at most, only a practical utility, we see that the motives which guided the scientific man are, from the beginning, manifestations of the aesthetic impulse.... The measure in which science falls short of art is the measure in which it is incomplete as science...

In a perceptive essay on Art and Science, the distinguished art critic, Roger Fry (who may be known to some of you through Virginia Woolf's biography of him), begins by quoting Sullivan and continues:

Sullivan boldly says: "It is in its aesthetic value that the justification of the scientific theory is to be found and with it the justification of the scientific method." I should like to pose to S. [Sullivan] at this point the question whether a theory that disregarded facts would have equal value for science with one which agreed with facts. I suppose he would say No; and yet so far as I can see there would be no purely aesthetic reason why it should not.

I shall return to this question which Roger Fry raises and suggest an answer different from what Fry presumes that Sullivan would have given. But I shall pass on now to Fry's observations comparing the impulses of an artist and of a scientist.

From the merest rudiments of pure sensation up to the highest efforts of design, each point in the process of art is inevitably accompanied by pleasure: it cannot proceed without it.... It is also true that the recognition of inevitability in thought is normally accompanied by pleasurable emotion; and that the desire for this mental pleasure is the motive force which impels to the making of scientific theory. In science the inevitability of the relations remains equally definite and demonstrable, whether the emotion accompanies it or not, whereas, in art, an aesthetic harmony simply does not exist without the emotional state. The harmony in art is not true unless it is felt with emotion.... In art the recognition of relations is immediate and sensational -- perhaps we ought to consider it as curiously akin to those cases of mathematical geniuses who have immediate intuition of mathematical relations which it is beyond their powers to prove....

Let me pass on from these generalities to particular examples of what scientists have responded to as beautiful.

My first example is related to Fry's observation with respect to what mathematical geniuses perceive as true with no apparent cause. The Indian mathematician, Srinivasa Ramanujan (whose dramatic emergence into mathematical fame in 1915 may be known to some of you) left a large number of notebooks (one of which was discovered only a few years ago). In these notebooks Ramanujan has recorded several hundred formulae and identities. Many of these have been proved only recently by methods which Ramanujan could not have known. G. N. Watson, who spent several years of his life proving many of Ramanujan's identities, has written:

Space Shuttle Over Greece, Turkey, & Aegean Sea

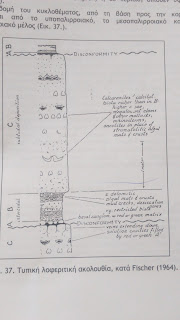
How do we correlate the Milankovitch orbital cycles to cyclochronology?

 Conceptual stratigraphic model 

Combined with the movement of perihelion (the time at which the Sun is closest to Earth), its frequency is about 20 thousand years, with two modes at 19 and 23 thousand years. Precession affects the timing of the seasons (when the seasons change). That is why we have to have a leap year every four: without this adjustment, in 10,000 years we would have spring in September instead of March in the northern Hemisphere, and vice versa. Modulated by eccentricity, precession is very important at low latitudes.


The following photographies are from Athens University Book of Geological Department, written by Professor Dr. Fotini A  Pomoni

Conseption about Kinetic Energy in Classical and relativistic mechanics

Pratik Sharma

Makawanpur multiple campus Hetauda,Nepal

LIGO-NOBEL

Ligo Nobel

The Odd Case of Quantum Black Holes

The Odd Case of Quantum Black Holes

Black Holes can be considered as some of the most mysterious yet fascinating objects in the universe. As they are usually portrayed in science fiction these astronomical riddles are the omnivores of the universe, consuming everything, even light, that dares to approach their observable boundary, aka the ”Event Horizon”, never to be seen again. In principle nothing can escape from them. Yet, as science has often done in the past, this consensus has been partially disproven by recent developments in quantum mechanics, as in its place arose a new problem also known as the information paradox which still to this day remains unresolved.

Introduction

1.1 The creation of a Black Hole

To understand what the problem is we must first take closer look to how black holes are formed. According to Einstein’s general theory of relativity if an object is compressed enough it can carve a region in space-time from which nothing can escape. But wait Jason! you might remark; Black holes are just stars that have died right? Well yes and no. Black Holes can indeed be massive stars that have ”died”, or to phrase it better stars that have went through a process called gravitational collapse in which the star literally contracts onto itself under the influence of its own gravity (why that happens now is an entirely different matter in and off itself and because I don’t want to blabber about something unrelated to the original subject of this article you can read more about it in this article by NASA:
 https://map.gsfc.nasa.gov/universe/rel stars.html),
 but giant stars are not the only things that can turn into black holes.

 Literally any object that is compressed down to what is called the Schwarzschild radius can turn into a black hole. The Schwarzschild radius is simply the radius of a sphere from which no information, no light, no particle can escape so that we can measure it (or so we thought, you’ll see what I mean later). The surface of that sphere is what we call the Event Horizon that I mentioned in the abstract. If the sun where to turn into a black hole it would have to be squeezed in a sphere with radius of about three kilometers! In the case that you would want to derive the Schwarzschild radius of anything you can simply use this equation: 

The only problem with creating a black hole is the amount of energy required to contract an object within such a small space, since the force to counteract the repulsive quantum forces between its subatomic particles is too great. Such energy is only observed in the gravitational collapses of giant stars of about six or seven solar masses, making black hole candidates scarce in the present universe. But here’s the catch, it turns out stellar collapse is not the only way to create black holes.

1.2 Primordial Black Holes

We generally know that the universe is expanding, decreasing in density, constantly, therefore it is safe to assume that in the past the average density was way way higher than today and in fact so high as to exceed the nuclear density of 2.3 × 1017 kg/m3 in the first microsecond of the life of the universe. The highest value of density that the universe could have started with is the so known Planck density, about 1097 g/cm3 , a density so high that even the fabric of space-time would break down. At these conditions black holes could have formed as small as 10−35 m across, also known as the Planck length, and with a mass of 10−8 kg, dimensions comparable to elementary particles. For all this incredible information we have to thank Stephen Hawking and Bernard J. Carr for their derivation of this mechanism for creating black holes[2]. 4 The fact that black holes could be so small intrigued Hawking, making him ponder about the possible quantum effects that could come into play in such a small scale. Thus came his famous conclusion of black holes emitting particles rather than just swallowing them[3].

2 Hawking Radiation

2.1 Emission and Evaporation

How can a black hole emit particles and why should it do that? A strange question indeed and difficult to answer at that. To make sense of this situation we must first take a look at some of quantum mechanics most basic principles.

 2.1.1 Vacuum Fluctuation

Heisenberg’s uncertainty principle states that one cannot know in great detail and in the same time the exact position and speed of a particle, or - from a more mathematical viewpoint - the product of the uncertainty of both position and momentum should always be greater than a certain value as seen in this inequality:

 ∆x∆p ≥ ¯h /2 

Where ¯h is the reduced Planck constant ( h /2π or 1.054×10−34m2kg/s). 

This relation has also been derived[4] in a energy/time form:

∆E∆t ≥ ¯h /2 

which means that in any point in space there must always be a minimal change in energy no matter how small or ”empty” this space is. Such a realization is very important because it necessitates that a vacuum can never truly be a vacuum, as in containing nothing, meaning that a small amount of energy should be created and later destroyed in order to fill this empty space. Wow slow down there! What about the conservation of energy? Energy cannot be created nor destroyed! Worry not, everything is fine since Quantum Mechanics show us that there is no violation of the law when we measure very short instances of time, thus the uncertainty of energy is incredibly high.

2.1.2 Particle Pairs

Many of you might be baffled by the fact that particles can both appear from and disappear into nothing but stay with me since this is a very important property of particles and it directly leads us to why black holes emit matter.

 Einstein has generously provided us with a very important equation, the famous 

E = mc2 , 

that shows us that energy and mass are just two faces of the same coin. Therefore if energy can pop into existence as the energy/time uncertainty principle dictates, then mass can too. If in a small space where one would consider to be a true vacuum suddenly appears a particle for a short moment and if that particle happens to disappear after this time has passed then there is a change in the energy in the space and so the uncertainty principle is satisfied. This happens all the time in space, constantly particles pop in existence only to disappear a moment later, filling space with energy fluctuations. An important requirement for such an event to unfold is that not only one particle appears but actually two, one made of matter and one of antimatter. That way particles would annihilate each other after a small amount of time. These particles are known as virtual particles. Also we must clarify that one of two particles has negative energy thus (stay with me) negative mass. This will be important in the next part of the article.

2.1.3 Radiation and Black Hole Temperature

If virtual particles come into existence extremely close to the surface of a black hole, even closer than the photon sphere (a spherical cortex on which light literally can orbit the black hole), then there is a chance that the particle pair will not annihilate itself but rather the particles will part ways, one escaping the black hole and the other falling into it. If the second one happens to be the one with negative mass then the net mass of the black hole decreases, and since we cannot see the negative mass particle as it has fallen into the hole we would only see the bizarre effect of the black hole shrinking accompanied by an emission of a particle than in actuality was just the part of the pair that survived. Some of you may point out the fact that in the grand scheme of things, there should be an equal chance of both the negative mass particle and the positive mass particle to fall into the black hole. That is not the case and the reasoning for the phenomenon takes us back to the world of Thermodynamics. The 6 second law of Thermodynamics states that the entropy of an isolated system (Entropy being the measure of disorder in the universe [5]) must always increase or stay at an equilibrium. Thus in a statistical view of the system there is a higher chance that the negative mass particle will plunge into the black hole, as this action will increase the entropy of both the system and consequently the universe.

,https://physics.stackexchange.com/users/1492/anna-v

Nevertheless, what we must take from all this is that we see that the black hole has the ability to radiate particles in a way very reminiscent of to what we know as temperature. Hawking in his work to study the effects of quantum mechanics on the surface of a black hole he derived a formula[3] also that shows that the temperature of a black hole is inversely proportional to the mass of the black hole, meaning a small black hole emits more energy than a big one. The formula he derived is this:

which shows us that its proportional to the hole’s mass. As the hole decreases in size it evaporates energy faster and in greater amounts until it gets so small that the amount of energy that needs to be released is so great and it has to be released in such a small amount of time that the hole literally explodes with more power than a million-megaton nuclear bomb! Of course these formulas are only approximations since a lot more things come into play when dealing with real life black holes like the radiation from the Cosmic Microwave Background or random matter falling into the black hole.

2.2 Leading to the information paradox

Hawking’s work is incredibly important and praise worthy as he connected three seemingly unrelated areas of physics, these being Relativity, Quantum Mechanics and Thermodynamics. Unfortunately this is the part that I introduce the problem that I mentioned in the abstract, the infamous information paradox, that took the physics society by storm.

3 The Information Paradox

3.1 Relativity versus Quantum Mechanics

3.1.1 The essence of information 

 In physics the term information is not really something tangible, but it must not be mistaken for not being well defined. Physical information can be defined as the complete wavefunction of a particle or just all of the properties of the particle (these being charge, spin, mass etc.). This definition can be expanded to an arrangement of particles, denoting to the way that the individual particles are connected and interact with each other.

 A very good example of this way of thinking has been recently introduced by the YouTube channel Kurzgesagt in their recent video ”Why Black Holes Could Delete The Universe The Information Paradox”[6]. In their video they say that if you arrange a bunch of carbon atoms in a certain way you will get coal but if you arrange them in a different way you get diamond, therefore information is just a property of the arrangement of these atoms. A very important law that also has to be stated is the conservation of information, that is that information cannot be destroyed (some- 8 thing that was derived by the quantum field theory and Liouville’s theorem). It can be separated to small pieces that are very hard to measure accurately (like burning a piece of paper and then trying to reconstruct the original by measuring every single change that underwent with every single molecule), or it can be stored somewhere that is not accessible by the laws of physics i.e. the surface of a black hole.

3.1.2 The contradiction

The paradox that arose by the conjecture of hawking radiation stems from the fact that information is ”lost” when falling into a black hole according to relativity. But if the black hole evaporates its mass away completely what happens to the mass inside? Information cannot be destroyed according to quantum mechanics but that is what would happen if a black hole where to evaporate completely. What is going on here? Hawking strongly believed in his theory and supported it firmly, suggesting that information is indeed lost. A conviction of this scale is frightening since it can mean that our current understanding of physics is so deeply mistaken that we would need to scrap all of the efforts of thousands of physicists across history out of the window and force us to start over.

3.2 Other Solutions

Only recently physicists have come up with possible ways to cut this gordian knot, with propositions like the black hole leaving a remnant of information after its death or creating an entirely new universe briefly before its death to store the information or it just leaks out the information over time. Still all of those hypotheses are yet to be proved since we have not yet seen a black hole evaporate, as we do not have the proper equipment for such a feat in our current technological state.

 References

[1] M.L. Kutner. Astronomy: A Physical Perspective. Cambridge University Press, 2003. 

[2] B. J. Carr and S. W. Hawking. Black holes in the early Universe. Monthly Notices of the Royal Astronomical Society, 168:399–416, aug 1974.

 [3] Stephen W Hawking. Particle creation by black holes. Communications in mathematical physics, 43(3):199–220, 1975.

 [4] J S Briggs. A derivation of the time-energy uncertainty relation. Journal of Physics: Conference Series, 99(1):012002, 2008.

 [5] J. Gribbin, M. Gribbin, and J. Gribbin. Q is for Quantum: An Encyclopedia of Particle Physics. Touchstone, 2000. 

[6] Kurzgesagt In a Nutshell. Why Black Holes Could Delete The Universe The Information Paradox. youtu.be/yWO-cvGETRQ, August 2017. 

Jason A. Andronis 

Physics Department, University of Crete

 September 24, 2017 

Floating water bridge between two beakers

A PASSION FOR SYMMETRY: ANTIMATTER LIGHT SPECTRUM

A PASSION FOR SYMMETRY: ANTIMATTER LIGHT SPECTRUM: Bohr Model     Bohr atomic model, description of the structure of atoms, especially that of hydrogen, proposed (1913) by the Danish ph...

ACCELERATING EDUCATION: FEYNMAN

ACCELERATING EDUCATION: FEYNMAN: Πράγματι, όπως εκτίμησε και ίδιος ο Feynman στον πρόλογο του από τις διαλέξεις φυσικής, όταν διαπίστωσε ότι ο αριθμός των φοιτητών του ...

ACCELERATING EDUCATION: URBAN GEOLOGY

ACCELERATING EDUCATION: URBAN GEOLOGY: improve the quality of life in urban areas This data set illustrates the geoscience information of the Ottawa/Outaouais (Ontario/Québe...

Pavement geology

pavement geology

The Largest Dam in The World affects the momentum of earth's inertia.

Cassini’s 13 years of stunning Saturn

CASSINI WILL STOP ITS TRIP SOON

you can read more at Nature Volume548 issue 7669 

Cassini’s 13 years of stunning Saturn science — in pictures

CONTACT WITH ALIEN

Link

ACCELERATING EDUCATION: Greek manuscript from Newton

ACCELERATING EDUCATION: Greek manuscript from Newton: Newton knew Greek and he used writing in Greek language at  his note book   see more at the link:   University of Cambridge









Newton was thinking in a different way, he believed in gravity. Gravity  was something magic for the most people in his life time.He wrote 500.000 words about  alchemυ.

ACCELERATING EDUCATION: relativistic baseball

ACCELERATING EDUCATION: relativistic baseball: http://what-if.xkcd.com/1/

ACCELERATING EDUCATION: 1st LESSON - Mechanics

ACCELERATING EDUCATION: 1st LESSON - Mechanics: Galileo Galilei   Galileo designed accurate sketches of moon. He inspired the theory of pendulum in the church. He calculated ...

DARK MATTER AND ENERGY

News

ACCELERATING EDUCATION: Snapchat and Physics

ACCELERATING EDUCATION: Snapchat and Physics: Live Experiments: acceleratingedu https://www.snapchat.com/add/acceleratingedu

A PASSION FOR SYMMETRY: WHAT IF THE ALIEN IS MADE BY ANTI-MATTER?

A PASSION FOR SYMMETRY: WHAT IF THE ALIEN IS MADE BY ANTI-MATTER?

ACCELERATING EDUCATION: URBAN GEOLOGY

ACCELERATING EDUCATION: URBAN GEOLOGY: This data set illustrates the geoscience information of the Ottawa/Outaouais (Ontario/Québec) area including geological history, subsurface ...

Θεματικές ασκήσεις μέσα και έξω απο το εργαστήριο.

Αποκτήστε το

ΤΟ ΠΕΙΡΑΜΑ ΤΟΥ ΕΡΑΤΟΣΘΕΝΗ

WALKING TO THE POLE, I FEEL LIKE A GIANT!!!

Προετοιμασία των επιλεγέντων Μαθητών για την την Ελληνική Συμμετοχή στην 48η Διεθνή Ολυμπιάδα Φυσικής 2017

GREECE

Time's Arrow

 A concept developed in 1927 by the British astronomer Arthur Eddington involving the "one-way direction" or "asymmetry" of time. Eddington  determined by studying the organization of  bodies that we can decide if an event happened normally or deversed



As an example we can see this video

What happens in the microkosmos?

SYMMETRIC PHENOMENA

ACCELERATING EDUCATION: Ταλαντώσεις Γ λυκείου Φυσικής

ACCELERATING EDUCATION: Ταλαντώσεις Γ λυκείου Φυσικής: Απόκτησε το

ACCELERATING EDUCATION: FEYNMAN

ACCELERATING EDUCATION: FEYNMAN: Πράγματι, όπως εκτίμησε και ίδιος ο Feynman στον πρόλογο του από τις διαλέξεις φυσικής
, όταν διαπίστωσε ότι ο αριθμός των φοιτητών του ...

ACCELERATING EDUCATION: FROM SPACE TO QUARK

ACCELERATING EDUCATION: FROM SPACE TO QUARK:              TRAVELING THROUGH THE UNIVERSE Nasa 1 Nasa 2 Nasa 3

THE DARK SIDE OF THE UNIVERSE: Theory of Everything- The quest for a big dream

THE DARK SIDE OF THE UNIVERSE: Theory of Everything- The quest for a big dream: Mysteries of the Standard Model (THE PHYSICS TEACHER ◆ Vol. 55, April 2017) Theory LQG predicts that both space and time decome quantiz...

Ο Φευνμαν προβλέπει την επικοινωνία με εξωγήινους!!!

A PASSION FOR SYMMETRY: Contact with an Alien: A PASSION FOR SYMMETRY: Contact with an Alien :             ΕΠΙΚΟΙΝΩΝΙΑ ΜΕ ΕΞΩΓΗΙΝΟ   Ο  διαπρεπής Αμερικανός ερευνητής  Joseph Henr...

Things the Standard Model does not explain

Things the Standard Model does not explain Despite those successes, there are quite a few features of the Universe not explained by the Standard Model. Why does the Universe contain matter but no antimatter? Why is the ’dark matter’, whose presence is needed to allow galaxies to form and to hold them together once they do? Why do observations show that the Universe’s expansion is presently accelerating? What causes irregularities in the density field of the primordial Universe, seen directly in the cosmic microwave background? These may be evidence of the need for new physics beyond the Standard Model.

A PASSION FOR SYMMETRY: A PASSION FOR SYMMETRY: Feynman Diagrams

A PASSION FOR SYMMETRY: A PASSION FOR SYMMETRY: Feynman Diagrams: A PASSION FOR SYMMETRY: Feynman Diagrams : FEYNMAN DIAGRAMS   May 11, 1918 – February 15, 1988 For his contributions to the...

A PASSION FOR SYMMETRY: A PASSION FOR SYMMETRY: Contact with an Alien

A PASSION FOR SYMMETRY: A PASSION FOR SYMMETRY: Contact with an Alien: A PASSION FOR SYMMETRY: Contact with an Alien :             ΕΠΙΚΟΙΝΩΝΙΑ ΜΕ ΕΞΩΓΗΙΝΟ   Ο  διαπρεπής Αμερικανός ερευνητής  Joseph Henr...

TIME DILATION GENERAL RELATIVITY

Time and intestellar 

1 hour in satellite  is 7 years in planet!!!